Understanding Transformers and GPT: An In-depth Overview
In this post, we delve into the technical details of the widely used transformer architecture by deriving all formulas involved in its forward and backward passes step by step. By doing so, we can implement these passes ourselves and often achieve more efficient performance than using autograd methods. Additionally, we introduce the technical details on the construction of the popular GPT-3 model using the transformer architecture.
Transformers $[1]$ are a type of neural network architecture designed to transform a sequence of $T$ input vectors,
\[\{ \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_T \} \;\;\;\;\;(\mathbf{x}_i \in \mathbb{R}^d, \; \forall i=1,2,\cdots,T),\]into an equal-length sequence of the so-called context-dependent output vectors:
\[\{ \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_T \} \;\;\;\;\;(\mathbf{y}_i \in \mathbb{R}^h, \; \forall i=1,2,\cdots,T).\]The output sequence in a transformer model is referred to as context-dependent because each output vector is influenced not only by the corresponding input vector but also by the context of the entire input sequence. Specifically, each output vector $\mathbf{y}_i$ depends on all input vectors in the sequence, not just $\mathbf{x}_i$ at the same position. As a result, each output vector can be viewed as a representation of not only the input vector at the same location but also its contextual information in the entire sequence.
More importantly, transformers utilize a flexible attention mechanism that enables them to generate each output vector $\mathbf{y}_i$ in a way that mainly relies on a certain number of the most relevant input vectors from anywhere in the input sequence, rather than just those input vectors near the position $i$. This ability to selectively attend to relevant information in the input sequence allows transformers to capture long-range dependencies and contextual information, making them a powerful tool for natural language processing and other sequential data tasks.
Transformers: Forward Pass
Let’s pack all input vectors as a $d \times T$ matrix, and all output vectors as an $l \times T$ matrix, as follows:
\[\mathbf{X} = \bigg[ \mathbf{x}_1 \; \mathbf{x}_2 \; \cdots \; \mathbf{x}_T \bigg]_{d \times T}\] \[\mathbf{Y} = \bigg[ \mathbf{y}_1 \; \mathbf{y}_2 \; \cdots \; \mathbf{y}_T \bigg]_{h \times T}\]In this way, a transformer can be viewed as a function $\cal{T}$ that maps from $\mathbf{X}$ to $\mathbf{Y}$:
\[\cal{T}: \;\;\; \mathbf{X} \longrightarrow \mathbf{Y}\]In the following, we will investigate all steps in the above mapping in a transformer.
- Forward step 1: we first introduce three parameter matrices $\mathbf{A}, \mathbf{B}, \mathbf{C} \in \mathbb{R}^{h \times d}$, which transform each input vector $\mathbf{x}_i$ to generate the so-called query vector $\mathbf{q}_i$, key vector $\mathbf{k}_i$, and value vector $\mathbf{v}_i$:
When the query, key, and value vectors are all derived from a common input source, we refer to the transformer’s mechanism as performing self-attention. Conversely, if these vectors are derived from different sources, the mechanism is called cross-attention.
The above operations can be combined as three matrix multiplications in the following:
\[\mathbf{Q} = \mathbf{A} \mathbf{X}, \;\; \mathbf{K} = \mathbf{B} \mathbf{X}, \;\; \mathbf{V} = \mathbf{C} \mathbf{X}\]where $\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{h \times T}$ are constructed by lining up the above vectors $\mathbf{q}_i$, $\mathbf{k}_i$ and $\mathbf{v}_i$ column by column.
- Forward step 2: use the above query and key vectors to compute all pair-wise attention between any two input vectors $\mathbf{x}_i$ and $\mathbf{x}_t$ ($\forall i,t =1,2, \cdots, T$) as follows:
Next, we normalize each $c_{it}$ with respect to all $i$ using the softmax function as follows:
\[a_{it} = \frac{e^{c_{it}}}{\sum_{j=1}^T \; e^{c_{jt}}} \;\;\;\;\;\;\;\;(\forall i,t =1,2, \cdots, T)\]We can pack all operations in this step into the following matrix operation:
\[\mathcal{A} = \textrm{softmax}\big(\mathbf{Q}^\intercal \mathbf{K}/\sqrt{h} \big) \;\;\;\;\;\; (\mathcal{A} \in \mathbb{R}^{T \times T})\]where the softmax operation is applied to the underlying matrix column-wise.
- Forward step 3: use the above $a_{it}$ as the attention coeffificents to generate an context-dependent vector from all value vectors:
We can represent the above as the following matrix multiplication:
\[\mathbf{Z} = \mathbf{V} \mathcal{A} = \mathbf{V} \; \textrm{softmax}\big(\mathbf{Q}^\intercal \mathbf{K}/\sqrt{h} \big)\]When transformers are employed as decoders to produce tokens, we typically utilize a form of attention known as causal attention. This attention mechanism ensures that each output vector is influenced solely by the input vectors that precede it, rather than any vectors that appear later in the sequence. In this case, we generate each $\mathbf{z}_t$ as
\[\mathbf{z}_t = \sum_{i=1}^t \; a_{it} \mathbf{v}_i \;\;\;\;\;\;\;\;(\forall t = 1,2,\cdots,T)\]To compute causal attention in matrix form, an upper-triangular matrix is employed to mask the attention matrix $\mathcal{A}$. This masking ensures that the attention mechanism only attends to previous positions in the sequence, as represented by the upper-triangular elements of the attention matrix, while ignoring future positions represented by the lower-triangular elements.
- Forward step 4: apply the layer normalization and one layer of fully-connected feedforward neural network to each $\mathbf{z}_t$ to generate the final output vector $\mathbf{y}_t$ as follows (note that residual connections $[2]$ are introduced here to facilitate optimization during learning):
where two more parameter matrices $\mathbf{W}_1 \in \mathbb{R}^{h’ \times h}$ and $\mathbf{W}_2 \in \mathbb{R}^{h \times h’}$ are introduced here. For convenience, we can use the following compact matrix form to represent all operations in this step:
\[\mathbf{Y} = \mathbf{X} + \textrm{LN}_{\gamma,\beta} \big( \mathbf{Z} \big) +\textrm{feedforward} \Big( \mathbf{X} + \textrm{LN}_{\gamma,\beta} \big( \mathbf{Z} \big)\Big).\]In summary, we can illustrate all attention operations in the forward pass of a transformer using matrices as in Figure 1.
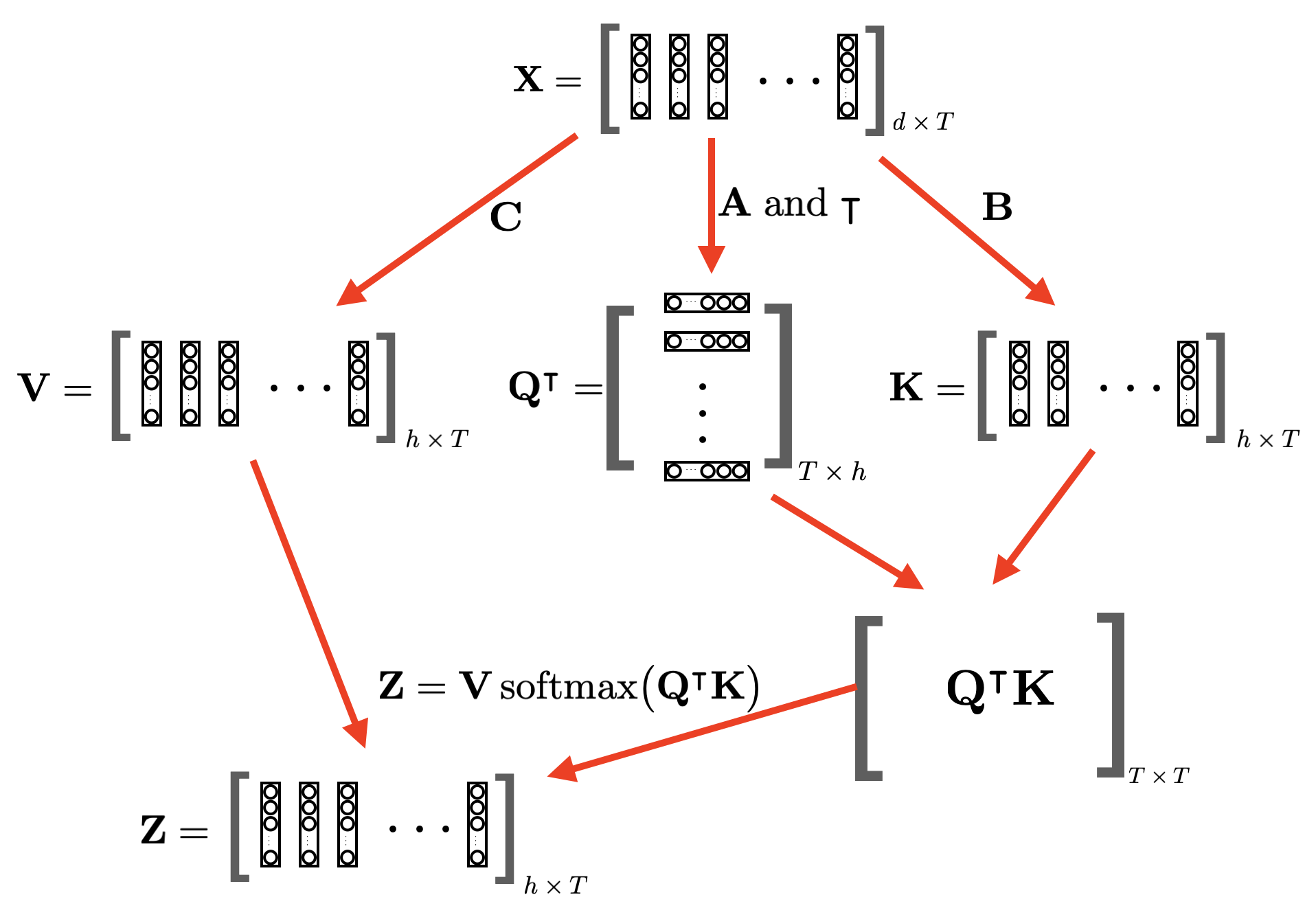
Transformers: Backward Pass
Let us now examine how to perform the backward pass to propagate errors in a transformer as well as how to compute the gradients of all transformer parameter matrices, specifically for all attention operations illustrated in Figure 1. For the backward pass of layer normalization and fully-connected feedforward layer, readers are directed to section 8.3.2 in reference $[3]$.
Assuming we possess error signals for the transformer outputs with respect to a particular objective function $F(\cdot)$, these signals are given as follows:
\[\mathbf{e}_t \overset{\Delta}{=} \frac{\partial F}{ \partial \mathbf{z}_t} \;\;\;\;\;\; (\forall t = 1, 2, \cdots, T)\]Arrange them column by column as a matrix:
\[\mathbf{E} = \frac{\partial F}{\partial \mathbf{Z}} = \left[ \;\; \frac{\partial F}{ \partial \mathbf{z}_t} \;\; \right]_{h \times T}\]Let’s break down all attention operations in a transformer in Figure 1 step by step backwards from the output towards input as follows:
- Backward step 1: we have
According to the chain rule, we can compute
\[\frac{\partial F}{\partial a_{it} } = \frac{\partial F}{\partial \mathbf{z}_t } \frac{\partial \mathbf{z}_t}{ \partial a_{it}} = \mathbf{v}_i^\intercal \frac{\partial F}{\partial \mathbf{z}_t } \;\;\;\;\;(\forall i,t=1,2,\cdots,T)\]Align all of these ($T^2$ terms in total) as a $T \times T$ matrix:
\[\left[ \;\; \frac{\partial F}{\partial a_{it}} \;\; \right]_{T \times T } = \bigg[ \;\; \mathbf{V}^\intercal \;\; \bigg]_{T\times h } \bigg[ \;\; \mathbf{E} \;\; \bigg]_{h \times T }\]- Backward step 2: we normalize as $a_{it} = \frac{e^{c_{i}t}}{\sum_{j=1}^T e^{c_{jt}}} \;\;\;\;\;\; (\forall i,t = 1,2, \cdots, T)$.
We denote
\[\mathbf{a}_t \overset{\Delta}{=} \big[ a_{1t} \, a_{2t} \, \cdots, a_{Tt} \big]^\intercal \;\;\;\;\; \textrm{and} \;\;\;\; \mathbf{c}_t \overset{\Delta}{=} \big[ c_{1t} \, c_{2t} \, \cdots, c_{Tt} \big]^\intercal\] \[\frac{\partial F}{\partial \mathbf{a}_t } \overset{\Delta}{=} \big[ \frac{\partial F}{\partial a_{1t}} \, \frac{\partial F}{\partial a_{2t}} \, \cdots \, \frac{\partial F}{\partial a_{Tt}} \big]^\intercal \;\;\;\;\; \textrm{and} \;\;\;\; \frac{\partial F}{\partial \mathbf{c}_t } \overset{\Delta}{=} \big[ \frac{\partial F}{\partial c_{1t}} \, \frac{\partial F}{\partial c_{2t}} \, \cdots \, \frac{\partial F}{\partial c_{Tt}} \big]^\intercal\]According to Eq.(8.14) on page 180 in $[3]$, for any $t=1,2,\cdots,T$, we have
\[\frac{\partial F}{\partial \mathbf{c}_t } = \mathbf{J}_{\tiny sm}(t) \; \frac{\partial F}{\partial \mathbf{a}_t } \;\;\;\;\; (\forall t=1,2,\cdots,T)\]with $\mathbf{J}_{\tiny sm}(t) = \textrm{diag} \big( \mathbf{a}_t \big) - \mathbf{a}_t \mathbf{a}_t^\intercal$. Furthermore, we use vector inner products to simplify the above matrix multiplications as follows:
\[\frac{\partial F}{\partial \mathbf{c}_t } = \mathbf{J}_{\tiny sm}(t) \; \frac{\partial F}{\partial \mathbf{a}_t } = \Big( \textrm{diag} \big( \mathbf{a}_t \big) - \mathbf{a}_t \mathbf{a}_t^\intercal \Big) \; \frac{\partial F}{\partial \mathbf{a}_t } = \mathbf{a}_t \odot \frac{\partial F}{\partial \mathbf{a}_t } - \big ( \mathbf{a}_t^\intercal \frac{\partial F}{\partial \mathbf{a}_t } \big)\mathbf{a}_t \;\;\;(\forall t=1,2,\cdots,T)\]where $\odot$ indicates element-wise multiplication of two vectors. Next, we align the above results column by column for all $t=1,2,\cdots, T$ and use the notation $\otimes$ to indicate the batch of all $T$ above operations as follows:
\[\left[ \;\;\;\; \frac{\partial F}{\partial \mathbf{c}_t } \;\;\;\; \right]_{T \times T } = \mathcal{A} \otimes \left[ \;\;\;\; \frac{\partial F}{\partial \mathbf{a}_t} \;\;\;\; \right]_{T \times T }\]It is worth noting that the aforementioned backward implementation can be applied directly to causal attention without any modifications.
- Backward step 3: due to $c_{it} = \mathbf{q}_i^\intercal \mathbf{k}_t/\sqrt{h} \;\;\;\;\;\; (\forall i,t = 1,2,\cdots, T)$, we have
Align these vectors column by column as the following matrix format:
\[\bigg[ \;\; \frac{\partial F}{ \partial \mathbf{q}_i} \;\; \bigg]_{h \times T} = \frac{1}{\sqrt{h}} \bigg[ \;\; \mathbf{K} \;\; \bigg]_{h \times T} \left[ \;\; \frac{\partial F}{\partial \mathbf{c}_t } \;\; \right]^\intercal_{T \times T }\]- Backward step 4: because of $\mathbf{q}_i = \mathbf{\mathbf{A}} \mathbf{x}_i$, we have
Putting all the above steps together, we have
\[\frac{\partial F}{\partial \mathbf{A}} = \frac{1}{\sqrt{h}}\bigg[ \;\; \mathbf{K} \;\; \bigg]_{h \times T} \Bigg( \mathcal{A} \otimes \Bigg( \bigg[ \;\; \mathbf{V}^\intercal \;\; \bigg]_{T\times h } \bigg[ \;\; \mathbf{E} \;\; \bigg]_{h \times T } \Bigg) \Bigg)^\intercal \bigg[ \;\; \mathbf{X}^\intercal \;\; \bigg]_{T\times d}\] \[= \frac{1}{\sqrt{h}} \mathbf{K} \bigg( \mathcal{A} \otimes \big( \mathbf{V}^\intercal \mathbf{E} \big) \bigg)^\intercal \mathbf{X}^\intercal\]Similarly, we can derive
\[\frac{\partial F}{\partial \mathbf{B}} = \frac{1}{\sqrt{h}} \mathbf{Q} \bigg( \mathcal{A} \otimes \big( \mathbf{V}^\intercal \mathbf{E} \big) \bigg) \mathbf{X}^\intercal\]Since we have
\[\mathbf{z}_t = \sum_{i=1}^T a_{it} \mathbf{v}_i\;\; (\forall t = 1,2, \cdots, T)\]We compute
\[\frac{\partial F}{ \partial \mathbf{v}_i} = \sum_{t=1}^T a_{it} \frac{\partial F}{\partial \mathbf{z}_t}\]Arrange them column by column into a matrix
\[\bigg[ \;\; \frac{\partial F}{ \partial \mathbf{v}_i} \;\;\bigg]_{h \times T} = \bigg[ \;\; \frac{\partial F}{ \partial \mathbf{z}_i} \;\;\bigg]_{h \times T} \bigg[ \;\; a_{it} \;\; \bigg]^\intercal_{T \times T} = \bigg[ \;\; \frac{\partial F}{ \partial \mathbf{z}_i} \;\;\bigg]_{h \times T} \mathcal{A}^\intercal = \mathbf{E} \mathcal{A}^\intercal\]Since we have $\mathbf{v}_i = \mathbf{C} \mathbf{x}_i \;\; (\forall i=1,2,\cdots,T)$ , we compute
\[\frac{\partial F}{\partial \mathbf{C}} = \sum_{i=1}^T \frac{\partial F}{\partial \mathbf{v}_i} \frac{\partial \mathbf{v}_i}{\partial \mathbf{C}} = \sum_{i=1}^T \frac{\partial F}{\partial \mathbf{v}_i} \mathbf{x}_i^\intercal = \bigg[ \;\; \frac{\partial F}{ \partial \mathbf{v}_i} \;\; \bigg]_{h \times T} \bigg[ \;\; \mathbf{X}^\intercal \;\; \bigg]_{T\times d}\]As a result, we have
\[\frac{\partial F}{\partial \mathbf{C }} = \mathbf{E} \mathcal{A}^\intercal \mathbf{X}^\intercal\]Finally, we back-propagate the error signals from output to input. The input $\mathbf{X}$ affects the output through three different paths, i.e. $\mathbf{Q}$, $\mathbf{K}$ and $\mathbf{V}$. Therefore, we have
\[\frac{\partial F}{\partial \mathbf{X}} = \frac{\partial F}{\partial \mathbf{Q}} \frac{\partial \mathbf{Q}}{ \partial \mathbf{X}} + \frac{\partial F}{\partial \mathbf{K}} \frac{\partial \mathbf{K}}{ \partial \mathbf{X}} + \frac{\partial F}{\partial \mathbf{V}} \frac{\partial \mathbf{V}}{ \partial \mathbf{X}}\] \[= \bigg[ \;\; \mathbf{A}^\intercal \;\; \bigg]_{d\times h} \bigg[ \;\; \frac{\partial F}{ \partial \mathbf{q}_i} \;\; \bigg]_{h \times T} + \bigg[ \;\; \mathbf{B}^\intercal \;\; \bigg]_{d\times h} \bigg[ \;\; \frac{\partial F}{ \partial \mathbf{k}_i} \;\; \bigg]_{h \times T} + \bigg[ \;\; \mathbf{C}^\intercal \;\; \bigg]_{d\times l}\bigg[ \;\; \frac{\partial F}{ \partial \mathbf{v}_i} \;\; \bigg]_{h \times T}\] \[= \frac{1}{\sqrt{h}} \bigg( \mathbf{A}^\intercal \mathbf{K} \Big( \mathcal{A} \otimes \big( \mathbf{V}^\intercal \mathbf{E} \big) \Big)^\intercal + \mathbf{B}^\intercal \mathbf{Q} \Big( \mathcal{A} \otimes \big( \mathbf{V}^\intercal \mathbf{E} \big) \Big) \bigg) + \mathbf{C}^\intercal \mathbf{E} \mathcal{A}^\intercal\]Finally, we summarize the above results using a more compact matrix representation. If we define the following $3h \times T$ matrix:
\[\mathbf{P} \overset{\Delta}{=} \begin{bmatrix} \frac{1}{\sqrt{h}} \mathbf{K} \bigg( \mathcal{A} \otimes \big( \mathbf{V}^\intercal \mathbf{E} \big) \bigg)^\intercal \\ \frac{1}{\sqrt{h}} \mathbf{Q} \bigg( \mathcal{A} \otimes \big( \mathbf{V}^\intercal \mathbf{E} \big) \bigg) \\ \mathbf{E} \mathcal{A}^\intercal \end{bmatrix}_{ 3h \times T}\]we have
\[\begin{bmatrix} \frac{\partial F}{\partial \mathbf{A}} \\[0.1cm] \frac{\partial F}{\partial \mathbf{B}} \\[0.1cm] \frac{\partial F}{\partial \mathbf{C}} \end{bmatrix} = \mathbf{P} \, \mathbf{X}^\intercal \;\;\;\;\;\;\Big(\in \mathbb{R}^{3h \times d} \Big)\] \[\frac{\partial F}{\partial \mathbf{X}} = \begin{bmatrix} \mathbf{A} \\ \mathbf{B} \\ \mathbf{C} \end{bmatrix}^\intercal \, \mathbf{P} = \Big[ \mathbf{A}^\intercal \;\; \mathbf{B}^\intercal \;\; \mathbf{C}^\intercal \Big] \, \mathbf{P} \;\;\;\;\;\;\Big(\in \mathbb{R}^{d \times T} \Big)\]Note: Refer to a pytorch implementation at Colab and its comparison with pytorch autograd (or a JAX implementation at Colab).
GPT-3
The authors of $[4]$ propose a deep multi-head transformer structure named GPT-3 for processing text data. In GPT-3, the values of $d$, $h$, and $T$ are set to $d=12288$, $h=128$, and $T=2048$, respectively, while the vocabulary is composed of $50257$ distinct tokens.
To begin, GPT-3 employs a tokenizer to split any text sequence into a sequence of tokens (each token is a common word fragment). These tokens are then transformed into vectors of $d=12288$ dimensions using a word embedding matrix $\mathbf{W}_0 \in \mathbb{R}^{12288 \times 50257}$. Subsequently, the input sequence $\mathbf{X} \in \mathbb{R}^{12288 \times 2048}$ is transformed into $\mathbf{Y} \in \mathbb{R}^{12288 \times 2048}$ using 96 layers of multi-head transformer blocks. Each block is defined as follows:
(1) Each multi-head transformer in GPT-3 uses $96$ heads:
\[\mathbf{A}^{(j)}, \mathbf{B}^{(j)}, \mathbf{C}^{(j)} \in \mathbb{R}^{128 \times 12288} \;\;\; (j=1,2, \cdots, 96)\]which compute for all $j=1,2,\cdots,T$:
\[\mathbf{Z}^{(j)} \in \mathbb{R}^{ 128 \times 2048} = \big( \mathbf{C}^{(j)} \mathbf{X} \big) \; \textrm{softmax}\Big( \big(\mathbf{A}^{(j)} \mathbf{X} \big)^\intercal \big( \mathbf{B}^{(j)} \mathbf{X} \big)/\sqrt{128}\Big)\](2) Concatenate the outputs from all heads:
\[\mathbf{Z} \in \mathbb{R}^{12288 \times 2048} = \mathbf{W}^o \textrm{concat}\big(\mathbf{Z}^{(1)}, \cdots, \mathbf{Z}^{(96)}\big)\]where $\mathbf{W}^o \in \mathbb{R}^{12288\times12288}$.
(3) Apply layer normalization to each column of $\mathbf{Z}$: $\mathbf{z}_t \in \mathbb{R}^{12288} \; (\forall t=1,2,\cdots,2048)$ as
\[\bar{\mathbf{z}}_t = \mathbf{x}_t + \textrm{LN}_{\gamma,\beta} \big(\mathbf{z}_t \big)\](4) Apply nonlinearity to each column as:
\[\mathbf{y}_t= \bar{\mathbf{z}}_t + \textrm{feedforward} \big( \bar{\mathbf{z}}_t\big) = \bar{\mathbf{z}}_t + \mathbf{W}_2 \textrm{ReLU} (\mathbf{W_1} \bar{\mathbf{z}}_t)\]where $\mathbf{W}_1 \in \mathbb{R}^{49152 \times 12288}$, and $\mathbf{W}_2 \in \mathbb{R}^{12288 \times 49152}$.
Based on these, we may calculate that the total number of parameters in GTP-3 is about $175$ billions.
During training, a sequence of training vectors
\[\{ \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_{2048} \}\]is fed into GPT-3 as input $\mathbf{X} \in \mathbb{R}^{12288\times 2048}$. For each time step $t=1,2,\cdots,2047$, GPT-3 is trained to predict the token at position $t+1$ based on all vectors appearing up to position $t$, i.e., ${\mathbf{x}_1, \cdots, \mathbf{x}_t}$.
After its training, GPT-3 has the ability to create new sequences by using an input sequence as a prompt. To do this, the model calculates the probabilities of the possible next tokens that could follow the given prompt, and then selects a new token by randomly sampling from these probabilities. The selected token is then added to the end of the prompt, forming a new prompt. This process continues until the model generates a termination token.
References
$[1]$ Ashish Vaswani, Noam Shazeer, et.al., Attention Is All You Need, arXiv, 1706,03762, 2017.
$[2]$ Kaiming He, Xiangyu Zhang, et.al., Deep Residual Learning for Image Recognition, arXiv, 1512,03385, 2015.
$[3]$ Hui Jiang, Machine Learning Fundamentals, Cambridge University Press, 2021.
$[4]$ Tom Brown and Benjamin Mann, et.al., Language Models are Few-Shot Learners, arXiv, 2005.14165, 2020.